Levers

source: hq-flash

This is a very relaxing game, by the independent developer Vectorpark. The game gives you different objects. Balance them out, to get a new one. There are also objects you can change and objects that will change in time.
.
.
.
.
.
.
source: jogueakiig

O criado deste game é Patrick Smith, um artista de flash inspirado que ficou conhecido por Vector Park, uma série de games de flash super viciantes baseados em obras de arte. No jogo você tem que equilibrar vários objetos diferente para conseguir alcançar o próximo nível. As peças vão cair uma a uma e você tem que encontrar uma maneira de deixá-las niveladas. Vale até retirar uma peça já posicionada para substituir por outra.
.
.
.
.
.
.
.
source: antimodal

It was created by Patrick Smith, and it has been around since at least May of 2001.

Spoilers below, so go play with it for a bit before you continue reading.

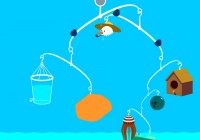
At first glance, it is not clear that this is a puzzle at all. Strange objects splash into the water at the bottom of the screen, and if you move the mouse over the tiny hooks you can retrieve the objects and attach them to the “lever” at the top. As soon as you attach an object, another will fall into the pool.

One soon determines that objects in the water will never sink beyond reach. In fact, whole structures of levers/hangers and objects can be dropped in the water without adverse effect. There are some strange physics here, as everything floats in the same way, just enough to be concealed from view. There’s no real purpose to this mechanism aside from inducing visual frustration.

The next thing to notice is that the objects can be rearranged, and only by rearranging the hangers and objects can you fit everything in. When everything is in place, the meter at the top of the screen turns into a timer. When the timer runs through a full cycle, a new object will drop. But sometimes, something will interrupt the timer. If the structure is lopsided, this seems to cause the problem. We’ll call this theory a.

Theory a: Keep the structure balanced.

After a little more experimentation it becomes clear that objects touching the water will interrupt the timer. This should be avoided.

Theory b: Keep hanging objects out of the water.

By about this time one has five hangers and five objects: a bowling ball, a submarine, a bucket with a faucet, a birdhouse, and a snowman. One can compare the relative weights of objects, and the bucket would be useful for this, but the faucet mechanism is awkward and the measurements very rough. One knows, though, that the submarine is heavier than the bowling ball, and the snowman is heavier than the submarine, and so on. Two or three birds are flapping around, perturbing the balance of things.

Theory c: A balanced structure must tolerate the effect of moving birds.

The next object is a squid. The squid weighs the same as the bowling ball, and as the empty birdhouse. The submarine equals the weight of two of those objects. The squid will propel itself upwards when it is too close to the water.

Theory c, revised: A balanced structure must tolerate the effects of moving birds and the squid.

Next comes a giant rock. The rock is very heavy, weighing more than a full bucket of water. It also changes color and makes a hissing sound when it touches the water — is this some kind of radioactive rock that heats up in the air? Oh, and the snowman appears to be melting — is that new, or has it been happening for a while? Well, holding the rock next to the snowman will melt everything but the hat.

Question d: I can melt the snowman. Should I?

The next object is the head of Zeus. (Well, it could be some other god, but Zeus seems the most likely choice.) The head is much heavier than everything else. To balance the head, one has to put Zeus on one side of the central hanger, and most everything else on the other side. But the depth of hangers on that other side is such that something is always dragging in the water. If we don’t balance the head this way, then the head will drag in the water. And there is still the snowman/empty hat to be positioned. There are too many objects.

Question d, revised: I need to get rid of an object. Where can I put the snowman’s hat?

The game offers a hint for what to do with the hat, as the snowman’s face will occasionally appear in the meter. And yes, the hat actually fits on that circle. Problem solved.

Theory d: Melt the snowman. Put the hat on the meter.

Okay, so now back to eight objects. Either Zeus is in the water, or something else is. But what about these hangers, do they weigh anything?

Theory e: The hangers have no weight.

This leads to a question:

Question f: Why are the hangers different widths?

The width of the hanger determines where the objects are positionally vertically as an effect of any tilt. A narrower hanger provides less vertical shift. What if one puts the Zeus head on a narrow hanger, as close the to top as possible?

While this satisfies Theory b, it weakens Theory a. Structural balance is not as important as keeping objects out of the water.

Theory f: Put the head on a the shortest hanger, just off the center hanger.

With so many hanging objects, the perturbations caused by the birds has little effect. The squid still seems to cause problems, though.

Theory c, re-revised: Ignore the birds. Don’t put the squid too close to the water.

To recap, the important theories are:

Theory b: Keep hanging objects out of the water.
Theory c, re-revised: Ignore the birds. Don’t put the squid too close to the water.
Theory d: Melt the snowman. Put the hat on the meter.
Theory f: Put the head on a the shortest hanger, just off the center hanger.

There are multiple arrangements which will complete the puzzle. The meter will turn into a sun, applause will sound, and Zeus’s eyes will light up.

Other things to try:

After the birds appear, drop everything in the water. There are only two spots on any hanger for birds to perch. If there is one hanger and three birds, one must stay in the air. Also, birds don’t like to perch in the same place twice.

The snowman’s hat appears to have negative weight.

Meta-puzzle: Why is this called “levers”? “Balance”, or “mobile” would make more sense.